在500个人身上试验某种血清预防感冒的作用，把一年中的记录与另外500个未用血清的人作比较，结果如下：未感冒感冒合计试验过252 248 500 未用过224 276 500 合计476 524 1000 根据上表数据，算得Χ2=3.14．以下推断正确的是（  ）

试卷相关题目

• 1为了研究子女吸烟与父母吸烟的关系，调查了1520青少年及其家长，得数据如下父母吸烟父母不吸烟合计 子女吸烟237 83 320 子女不吸烟678 522 1200 合计915 605 1520 附：经过独立性检验计算得K2的观测值k=≈32.52．附表：P（K2≥k） 0.050 0.010 0.001 k 3.841 6.635 10.828 参照附表，则下列结论较准确的一个是（  ）

  A.子女吸烟与父母吸烟无关

  B.有95%的把握说子女吸烟与父母吸烟有关

  C.有99%的把握说子女吸烟与父母吸烟有关

  D.有99.9%的把握说子女吸烟与父母吸烟有关

  开始考试点击查看答案
• 2为了检验某套眼睛保健操预防学生近视的作用，把500名做过该保健操的学生与另外500名未做该保健操的学生视力情况记录作比较，提出假设H0：“这套眼睛保健操不能起到预防近视的作用”，利用2×2列联表计算的K2≈3.918．经查对临界值表知P（K2≥3.841）=0.05．对此，四名同学做出了以下的判断：P：有95%的把握认为“这种眼睛保健操能起到预防近视的作用”；q．若某人未做眼睛保健操，那么他有95%的可能性得近视；r：这种眼睛保健操预防近视的有效率为95%；s：这种眼睛保健操预防近视的有效率为5%，则下列结论中，正确结论的序号是（  ）①p∧¬q；②¬p∧q；③（¬p∧¬q）∧（r∨s）；④（p∨¬r）∧（¬q∨s）．

  A.①③

  B.②④

  C.①④

  D.都不对

  开始考试点击查看答案
• 3统计中有一个非常有用的统计量k2，用它的大小可以确定在多大程度上可以认为“两个分类变量有关系”，下表是反映甲、乙两个平行班（甲班A老师教，乙班B老师教）进行某次数学考试，按学生考试及格与不及格统计成绩后的2×2列联表．不及格及格总计甲班（A教）4 36 40 乙班（B教）16 24 40 总计20 60 80 根据k2的值，你认为不及格人数的多少与不同老师执教有关系的把握大约为（  ）

  A.99.5%

  B.99.9%

  C.95%

  D.无充分依据

  开始考试点击查看答案
• 4某市政府调查市民收入增减与旅游欲望的关系时，采用独立性检验法抽查了3000人，计算发现K2=6.023，则根据这一数据查阅下表，市政府断言市民收入培养与旅游欲望有关系的可信程度是（  ）P（K2≥k） … 0.25 0.15 0.10 0.025 0.010 0.005 … k … 1.323 2.072 2.706 5.024 6.635 7.879 …  

  A.90%

  B.95%

  C.97.5%

  D.99.5%

  开始考试点击查看答案
• 5某班主任对全班50名学生进行了作业量多少的调查，数据如下表：认为作业多认为作业不多总数喜欢玩电脑游戏18 9 27 不喜欢玩电脑游戏8 15 23 总数26 24 50 根据表中数据得到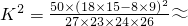5.059，参考下表：P（K2≥k） 0.050 0.025 0.010 0.001 k 3.841 5.024 6.635 10.828 则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为（  ）

  A.97.5%

  B.95%

  C.90%

  D.99.9%

  开始考试点击查看答案
• 6某同学对100名学生进行了喜欢运动与身体健康的关系的调查，数据如下表：喜欢运动不喜欢运动合计身体健康40 10 50 身体不健康30 20 50 合计70 30 100 参照下表P（K2≥k） 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 则认为喜欢运动与身体健康是否有关系的把握大约为（  ）参考公式：．

  A.90%

  B.95%

  C.99%

  D.99.9%

  开始考试点击查看答案
• 7在一次独立性检验中，得出列联表如下：A A1 合计B 200 800 1000 B1 180 a 180+a 合计380 800+a 1180+a 且最后发现，两个分类变量A和B没有任何关系，则a的可能值是（  ）

  A.200

  B.720

  C.100

  D.180

  开始考试点击查看答案