设方阵A有特征值λ且属于λ的特征向量ɑ，方阵B=P-1AP，则B有特征向量()。

您可能感兴趣的试题

• 1设λ=3是可逆矩阵A的一个特征值，则矩阵有一个特征值等于()。

  设λ=3是可逆矩阵A的一个特征值，则矩阵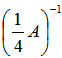有一个特征值等于()。

  　　 A

  　　B

  　　C

  　　D

  
  

  点击查看答案进入在线练题题不想做，我帮你做
• 2设，则A的属于特征值0的特征向量是()。

  设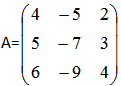，则A的属于特征值0的特征向量是()。

  　　A(1，1，2)T

  　　B(1，2，3)T

  　　C(1，0，1)T

  　　D(1，1，1)T

  
  

  点击查看答案进入在线练题题不想做，我帮你做
• 3矩阵A的特征值为1，则行列式的值等于()。

  矩阵A的特征值为1，则行列式的值等于()。

  　　A1

  　　B2

  　　C3

  　　D0

  
  

  点击查看答案进入在线练题题不想做，我帮你做
• 4设ɑ，β是n阶矩阵A的属于不同特征值的特征向量，则()。

  设ɑ，β是n阶矩阵A的属于不同特征值的特征向量，则()。

  　　Aɑ，β必正交

  　　Bɑ，β线性相关

  　　Cɑ，β线性无关

  　　D以上关系不一定成立

  
  

  点击查看答案进入在线练题题不想做，我帮你做
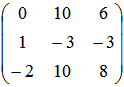• 5已知矩阵A=，且ɑ=是A的一个特征向量，则ɑ对应的特征值为()。

  已知矩阵A=，且ɑ=是A的一个特征向量，则ɑ对应的特征值为()。

  　　A1

  　　B-1

  　　C2

  　　D-2

  
  

  点击查看答案进入在线练题题不想做，我帮你做
• 6已知三阶矩阵A的特征值为1，2，3，则|A-5I|=()。

  已知三阶矩阵A的特征值为1，2，3，则|A-5I|=()。

  　　A2

  　　B6

  　　C-24

  　　D24

  
  

  点击查看答案进入在线练题题不想做，我帮你做
• 7不属于矩阵的特征向量是()。

  不属于矩阵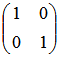的特征向量是()。

  　　A(0，0)’

  　　B(1，1)’

  　　C(1，0)’

  　　D(0，1)’

  
  

  点击查看答案进入在线练题题不想做，我帮你做
• 8设λ=-2是可逆矩阵A的特征值，则矩阵A-1+A有一特征值()。次型()

  设λ=-2是可逆矩阵A的特征值，则矩阵A-1+A有一特征值()。

  　　A

  　　B

  　　C0

  　　D

  
  

  点击查看答案进入在线练题题不想做，我帮你做
• 9实二次型为正定二次型的充要条件是()。

  实二次型为正定二次型的充要条件是()。

  　　A负惯性指数全为零

  　　B对任意向量，都是xTAx>0

  　　C|A|>0

  　　D存在n阶矩阵P，使A=PTP

  
  

  点击查看答案进入在线练题题不想做，我帮你做
• 10实二次型的符号差为()。

  实二次型的符号差为()。

  　　A0

  　　B1

  　　C2

  　　D3

  　　

  点击查看答案进入在线练题题不想做，我帮你做