如图所示,质量均为m的两块完全相同的木块A、B,放在一段粗糙程度相同的水平地面上,木块A、B间夹有一小块炸药(炸药的质量可以忽略不计)。让A、B以初速度v
0一起从O点滑出,滑行一段距离后到达P点,速度变为v
0/2,此时炸药爆炸使木块A、B脱离,发现木块B立即停在原位置,木块A继续沿水平方向前进。已知O、P两点间的距离为x,炸药爆炸时释放的化学能50%转化为木块的动能,爆炸时间很短可以忽略不计,求:
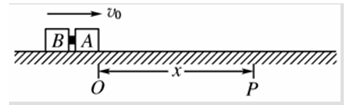
i. 木块与水平地面的动摩擦因数μ;
ii.炸药爆炸时释放的化学能。
答案 :
(1)
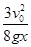
(2)
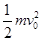
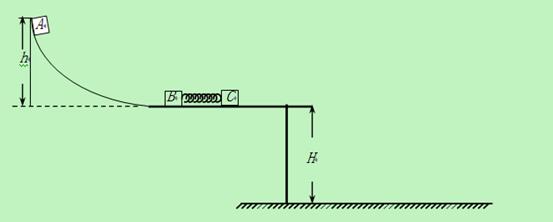
(14分)如图所示,一轻质弹簧的一端固定在滑块B上,另一端与滑块C接触但未连接,该整体静止放在离地面高为H=5m的光滑水平桌面上.现有一滑块A从光滑曲面上离桌面h=1.8m高处由静止开始滑下,与滑块B发生碰撞并粘在一起压缩弹簧推动滑块C向前运动,经一段时间,滑块C脱离弹簧,继续在水平桌面上匀速运动一段后从桌面边缘飞出. 已知m
A="1kg," m
B="2kg," m
C=3kg,g=10m/s
2,求:
(1)滑块A与滑块B碰撞结束瞬间的速度;
(2)被压缩弹簧的最大弹性势能;
(3)滑块C落地点与桌面边缘的水平距离.
答案 :
解:(14分)⑴ 滑块A从光滑曲面上h高处由静止开始滑下的过程,机械能守恒,设其滑到底面的速度为v1 ,由机械能守恒定律有:
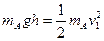
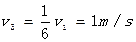
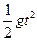
解之得:
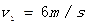
滑块A与B碰撞的过程,A、B系统的动量守恒,碰撞结束瞬间具有共同速度设为v2 ,由动量守恒定律有:
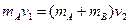
解之得:
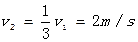
(2)滑块A、B发生碰撞后与滑块C一起压缩弹簧,压缩的过程机械能守恒,被压缩弹簧的弹性势能最大时,滑块A、B、C速度相等,设为速度
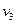
,
由动量守恒定律有:
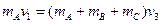
由机械能守恒定律有:
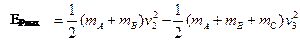
E="3J "
(3)被压缩弹簧再次恢复自然长度时,滑块C脱离弹簧,设滑块A、B的速度为
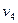
,滑块C的速度为
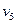
,分别由动量守恒定律和机械能守恒定律有:
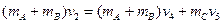
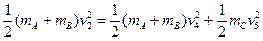
解之得:
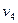
= 0,
V5="2m/s "
滑块C从桌面边缘飞出后做平抛运动:
S =
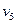
t
H=" "
解之得:S =" " 2m

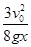 (2)
(2)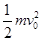

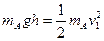
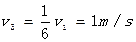
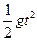
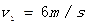
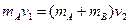
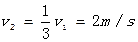
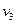 ,
,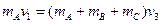
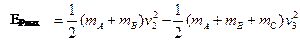
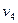 ,滑块C的速度为
,滑块C的速度为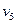 ,分别由动量守恒定律和机械能守恒定律有:
,分别由动量守恒定律和机械能守恒定律有: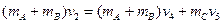
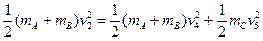
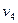 = 0,
= 0, 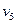 t
t
点击加载更多评论>>