已知点A(1,0),B(-1,0),过点C(0,-1)的直线l与线段AB相交,则直线l的倾斜角范围是( )
| A.[45°,135°] |
B.[45°,90°)∪(90°,135°] |
| C.[0°,45°]∪[135°,180°] |
D.[0°,135°] |
答案 : 如图所示:设直线l的倾斜角为α.
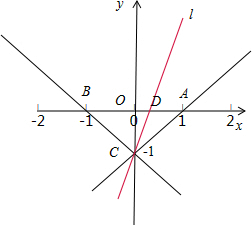
可求k
AC=
=1,kBC=
=-1.
要使直线l(CD)与线段AB相交,则k
l≥k
AC=1,或k
l≤k
BC=-1,
由tanα≥1,或tanα≤-1,0°<α<180°,解得45°≤α≤135°.
故选A.
直线kx-y=k-1与ky-x=2k的交点位于第二象限,那么k的取值范围是( )
| A.k>1 |
B.0<k<
|
C.k<
|
D.
<k<1 |
答案 : 当k=0时,直线方程可化为y=1,x=0,交点为(0,1),不在第二象限,故k≠0,
联立两直线方程得
,由②得y=
③,
把③代入①得:kx-
=k-1,
当k+1≠0即k≠-1时,解得x=,把x=
代入③得到y=
,
∴交点坐标为(
,
)
∵直线kx-y=k-1与直线ky=x+2k的交点在第二象限内,
∴
,解得0<k<1,k>1,或k<
,
∴k的取值范围是0<k<
故选B

点击加载更多评论>>