社会越来越浮躁,急功近利者比比皆是,当然也有像“数学考试大纲导读”那样的竟然预测准了几道考研题目者,但这并不普遍。考生要做的仍然是踏踏实实地复习好基础知识,不被外界的浮躁所感染与诱惑。
蝴蝶效应可用来解释微分方程对初值的依赖性,这是研究微分方程的定性问题中必会涉及的。而考研仅是对定量的研究,而且只是为数极少的能解出通解与特解的常微分方程进行研究解题方法。理论上极其简单,实践上也非常机械,可以是最易掌握的内容。但需要注意的是综合性问题,如微分方程与级数的结合等。
大纲中要求微分方程内容有:常微分方程的基本概念,变量可分离的微分方程,齐次微分方程,一阶线性微分方程,伯努利(Bernoulli)方程,全微分方程,可用简单的变量代换求解的某些微分方程,可降阶的高阶微分方程,线性微分方程解的性质及解的结构定理,二阶常系数齐次线性微分方程,高于二阶的某些常系数齐次线性微分方程,简单的二阶常系数非齐次线性微分方程,欧拉(Euler)方程,微分方程的简单应用
具体要求有:
了解微分方程及其阶、解、通解、初始条件和特解等概念。
掌握变量可分离的微分方程及一阶线性微分方程的求解方法。
会解齐次微分方程、伯努利方程和全微分方程,会用简单的变量代换解某些微分方程。
会用降阶法解下列形式的微分方程:
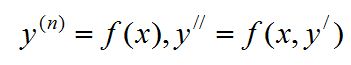
和
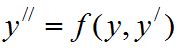
理解线性微分方程解的性质及解的结构定理。
掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程。
会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程。
会解欧拉方程。
会用微分方程解决一些简单的应用问题。
在这些内容与要求下,掌握一些常用的规则即可很容易解决相关问题。但需注意最基本运算的准确性。
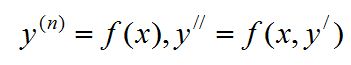
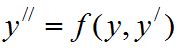
点击加载更多评论>>