2020江西农信社招聘考试行测备考:容斥问题考点及实例解析

　　一、容斥问题考点

　　1、集合与元素：把一类事物的全体放在一起就形成一个集合。每个集合总是由一些成员组成的，集合的这些成员，叫做这个集合的元素。

　　如：集合A={0，1，2，3，……，9}，其中0，1，2，…9为A的元素。

　　2、并集：由所有属于集合A或集合B的元素所组成的集合，叫做A，B的并集，记作A∪B，记号“∪”读作“并”。A∪B读作“A并B”，用图表示为图中阴影部分表示集合A，B的并集A∪B。

　　

 

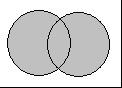
　　例：已知6的约数集合为A={1，2，3，6}，10的约数集合为B={1，2，5，10}，则A∪B={1，2，3，5，6，10}

　　3、交集：A、B两个集合公共的元素，也就是那些既属于A，又属于B的元素，它们组成的集合叫做A和B的交集，记作“A∩B”，读作“A交B”，如图阴影表示：

　　

 

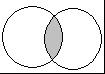
　　例：已知6的约数集合A={1，2，3，6}，10的约数集合B={1，2，5，10}，则A∩B={1，2}。

　　4、容斥原理(包含与排除原理)：

　　(用|A|表示集合A中元素的个数，如A={1，2，3}，则|A|=3)

　　原理一：给定两个集合A和B，要计算A∪B中元素的个数，可以分成两步进行：

　　第一步：先求出∣A∣+∣B∣(或者说把A，B的一切元素都“包含”进来，加在一起);

　　第二步：减去∣A∩B∣(即“排除”加了两次的元素)

　　总结为公式：|A∪B|=∣A∣+∣B∣-∣A∩B∣

　　原理二：给定三个集合A，B，C。要计算A∪B∪C中元素的个数，可以分三步进行：

　　第一步：先求∣A∣+∣B∣+∣C∣;

　　第二步：减去∣A∩B∣，∣B∩C∣，∣C∩A∣;

　　第三步：再加上∣A∩B∩C∣。

　　即有以下公式：

　　∣A∪B∪C∣=∣A∣+∣B∣+∣C∣-∣A∩B∣-∣B∩C∣- |C∩A|+|A∩B∩C∣

　　二、例题分析：

　　例1 求不超过20的正整数中是2的倍数或3的倍数的数共有多少个。

　　分析：设A={20以内2的倍数}，B={20以内3的倍数}，显然，要求计算2或3的倍数个数，即求∣A∪B∣。

　　解1：A={2，4，6，…20}，共有10个元素，即|A|=10

　　B={3，6，9，…18}，共有6个元素，即|B|=6

　　A∩B={既是2的倍数又是3的倍数}={6，12，18}，共有3个元素，即|A∩B|=3

　　所以∣A∪B∣=∣A∣+∣B∣-∣A∩B∣=10+6-3=13，即A∪B中共有13个元素。

　　解2：本题可直观地用图示法解答

　　

 

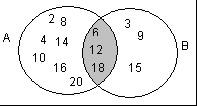
　　如图,其中,圆A中放的是不超过20的正整数中2的倍数的全体;圆B中放的是不超过20的正整数中3的倍数的全体,其中阴影部分的数6,12,18是既是2的倍数又是3的倍数的数(即A∩B中的数)只要数一数集合A∪B中的数的个数即可。

　　例2 某班统计考试成绩，数学得90分上的有25人;语文得90分以上的有21人;两科中至少有一科在90分以上的有38人。问两科都在90分以上的有多少人?

　　解：设A={数学成绩90分以上的学生}

　　B={语文成绩90分以上的学生}

　　那么，集合A∪B表示两科中至少有一科在90分以上的学生，由题意知，

　　∣A∣=25，∣B∣=21，∣A∪B∣=38

　　现要求两科均在90分以上的学生人数，即求∣A∩B∣，由容斥原理得

　　∣A∩B∣=∣A∣+∣B∣-∣A∪B∣=25+21-38=8

　　点评：解决本题首先要根据题意，设出集合A，B，并且会表示A∪B，A∩B，再利用容斥原理求解。

　　例3 某班同学中有39人打篮球，37人跑步，25人既打篮球又跑步，问全班参加篮球、跑步这两项体育活动的总人数是多少?

　　解：设A={打篮球的同学};B={跑步的同学}

　　则 A∩B={既打篮球又跑步的同学}

　　A∪B={参加打篮球或跑步的同学}

　　应用容斥原理∣A∪B∣=∣A∣+∣B∣-∣A∩B∣=39+37-25=51(人)

　　例4 求在不超过100的自然数中，不是5的倍数，也不是7的倍数有多少个?

　　分析：这个问题与前几个例题看似不相同，不能直接运用容斥原理，要计算的是“既不是5的倍数，也不是7的倍数的数的个数。”但是，只要同学们仔细分析题意，这只需先算出“100以内的5的倍数或7的倍数的数的个数。”再从100中减去就行了。

　　解：设A={100以内的5的倍数}

　　B={100以内的7的倍数}

　　A∩B={100以内的35的倍数}

　　A∪B={100以内的5的倍数或7的倍数}

　　则有∣A∣=20，∣B∣=14，∣A∩B∣=2

　　由容斥原理一有：∣A∪B∣=∣A∣+∣B∣-∣A∩B∣=20+14-2=32

　　因此，不是5的倍数，也不是7的倍数的数的个数是：100-32=68(个)

　　点评：从以上的解答可体会出一种重要的解题思想：有些问题表面上看好象很不一样，但经过细心的推敲就会发现它们之间有着紧密的联系，应当善于将一个问题转化为另一个问题。

　　例5 某年级的课外学科小组分为数学、语文、外语三个小组，参加数学小组的有23人，参加语文小组的有27人，参加外语小组的有18人;同时参加数学、语文两个小组的有4人，同时参加数学、外语小组的有7人，同时参加语文、外语小组的有5人;三个小组都参加的有2人。问：这个年级参加课外学科小组共有多少人?

　　解1：设A={数学小组的同学}，B={语文小组的同学}，C={外语小组的同学}，A∩B={数学、语文小组的同学}，A∩C={参加数学、外语小组的同学}，B∩C={参加语文、外语小组的同学}，A∩B∩C={三个小组都参加的同学}

　　由题意知：∣A∣=23，∣B∣=27，∣C∣=18

　　∣A∩B∣=4，∣A∩C∣=7，∣B∩C∣=5，∣A∩B∩C∣=2

　　根据容斥原理二得：

　　∣A∪B∪C∣=∣A∣+∣B∣+∣C∣-∣A∩B∣-∣A∩C|-∣B∩C|+|A∩B∩C∣

　　=23+27+18-(4+5+7)+2

　　=54(人)

　　解2： 利用图示法逐个填写各区域所表示的集合的元素的个数，然后求出最后结果。

　　

 

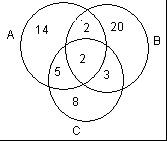
　　设A、B、C分别表示参加数学、语文、外语小组的同学的集合，其图分割成七个互不相交的区域，区域Ⅶ(即A∩B∩C)表示三个小组都参加的同学的集合，由题意，应填2。区域Ⅳ表示仅参加数学与语文小组的同学的集合，其人数为4-2=2(人)。区域Ⅵ表示仅参加数学与外语小组的同学的集合，其人数为7-2=5(人)。区域Ⅴ表示仅参加语文、外语小组的同学的集合，其人数为5-2=3(人)。区域Ⅰ表示只参加数学小组的同学的集合，其人数为23-2-2-5=14(人)。同理可把区域Ⅱ、Ⅲ所表示的集合的人数逐个算出，分别填入相应的区域内，则参加课外小组的人数为：

　　14+20+8+2+5+3+2=54(人)

　　点评：解法2简单直观，不易出错。由于各个区域所表示的集合的元素个数都计算出来了，因此提供了较多的信息，易于回答各种方式的提问。

　　例6 学校教导处对100名同学进行调查，结果有58人喜欢看球赛，有38人喜欢看戏剧，有52人喜欢看电影。另外还知道，既喜欢看球赛又喜欢看戏剧(但不喜欢看电影)的有6人，既喜欢看电影又喜欢看戏剧(但不喜欢看球赛)的有4人，三种都喜欢的有12人。问有多少同学只喜欢看电影?有多少同学既喜欢看球赛又喜欢看电影(但不喜欢看戏剧)?(假定每人至少喜欢一项)

　　解法1：画三个圆圈使它们两两相交，彼此分成7部分(如图)这三个圆圈分别表示三种不同爱好的同学的集合，由于三种都喜欢的有12人，把12填在三个圆圈的公共部分内(图中阴影部分)，其它6部分填上题目中所给出的不同爱好的同学的人数(注意，有的部分的人数要经过简单的计算)其中设既喜欢看电影又喜欢看球赛的人数为χ，这样，全班同学人数就是这7部分人数的和，即

　　16+4+6+(40-χ)+(36-χ)+12=100

　　解得 χ=14

　　只喜欢看电影的人数为

　　36-14=22

　　

 

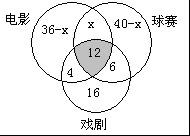
　　解法2：设A={喜欢看球赛的人}，B={喜欢看戏剧的人}，C={喜欢看电影的人}，依题目的条件有|A∪B∪C|=100，|A∩B|=6+12=18(这里加12是因为三种都喜欢的人当然喜欢其中的两种)，|B∩C|=4+12=16，|A∩B∩C|=12，再设|A∩C|=12+χ由容斥原理二：|A∪B∪C |=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|

　　得：100=58+38+52-(18+16+х+12)+12

　　解得：х=14

　　∴36-14=22

　　所以既喜欢看电影又喜欢看球赛的人数为14，只喜欢看电影的人数为22。

　　点评：解法1没有用容斥原理公式，而是先分别计算出(未知部分设为х)各个部分(本题是7部分)的数目，然后把它们加起来等于总数，这种计算方法也叫“分块计数法”，它是利用图示的方法来解决有关问题，希望同学们能逐步掌握此类方法，它比直接用容斥原理公式更直观，更具体。

　　例7、某车间有工人100人，其中有5个人只能干电工工作，有77人能干车工工作，86人能干焊工工作，既能干车工工作又能干焊工工作的有多少人?

　　解：工人总数100，只能干电工工作的人数是5人，除去只能干电工工作的人，这个车间还有95人。 利用容斥原理，先多加既能干车工工作又能干焊工工作的这一部分，其总数为163，然后找出这一公共部分，即163-95=68

　　例8、某次语文竞赛共有五道题(满分不是100分)，丁一只做对了(1)、(2)、(3)三题得了16分;于山只做对了(2)、(3)、(4)三题，得了25分;王水只做对了(3)、(4)、(5)三题，得了28分，张灿只做对了(1)、(2)、(5)三题，得了21分，李明五个题都对了他得了多少分?

　　解：由题意得：前五名同学合在一起，将五个试题每个题目做对了三遍，他们的总分恰好是试题总分的三倍。五人得分总和是16+25+28+21=90。因此，五道题满分总和是90÷3=30。所以李明得30分。

　　例9，某大学有外语教师120名，其中教英语的有50名，教日语的有45名，教法语的有40名，有15名既教英语又教日语，有10名既教英语又教法语，有8名既教日语又教法语，有4名教英语、日语和法语三门课，则不教三门课的外语教师有多少名?

　　解：本题只有求出至少教英、日、法三门课中一种的教师人数，才能求出不教这三门课的外语教师的人数。至少教英、日、法三门课中一种教师人数可根据容斥原理求出。根据容斥原理,至少教英、日、法三门课中一种的教师人数为50+45+40-15-10-8+4=106(人)不教这三门课的外语教师的人数为120-106=14(人)。