数学：空间向量与立体几何经典例题

已知P是△ABC所在平面内一点，

PB

+

PC

+2

PA

=

0

，现将一粒黄豆随机撒在△ABC内，则黄豆落在△PBC内的概率是（　　）

A． 1 4

B． 1 3

C． 1 2

D． 2 3

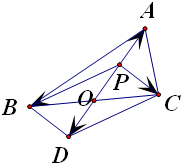
答案 : 以PB、PC为邻边作平行四边形PBDC，则

PB

+

PC

=

PD

∵

PB

+

PC

+2

PA

=

0

，
∴

PB

+

PC

=-2

PA

，得

PD

=-2

PA

由此可得，P是△ABC边BC上的中线AO的中点，
点P到BC的距离等于A到BC的距离的

1

2

．
∴S_△PBC=

1

2

S_△ABC．
将一粒黄豆随机撒在△ABC内，黄豆落在△PBC内的概率为P=

S△PBC

S△ABC

=

1

2

故选C
设A，B，C为单位圆O上不同的三点，则点集A={(x，y)|

OC

=x

OA

+y

OB

，0＜x＜2，0＜y＜2}所对应的平面区域的面积为（　　）

A．1

B． 3 2

C．2

D． 5 2

答案 : 将

OC

=x

OA

+y

OB

两边平方得：

OC

2=x2

OA

2+y2

OB

2+2xy

OA

•

OB

cos∠AOB．
∵|

OA

|=|

OB

|=|

OC

|=1，
∴1=x²+y²+2xycos∠AOB，
∵0＜x＜2，0＜y＜2．
从而由余弦定理可知x、y、1可以构成三角形，且∠AOB不是0°或180°．
于是有：

|x|+|y|≥1 |x|+1≥|y| |y|+1≥|x| 0＜x＜2，0＜y＜2

，化为 

x+y≥1 x+1≥y y+1≥x 0＜x＜2，0＜y＜2

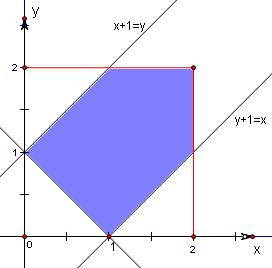
画出平面区域，结合图形可知约束条件表示的图形为阴影区域内，
∴表示的平面区域的面积是4-3×

1

2

=

5

2

．
故答案为：

5

2

．