- 讲师:刘萍萍 / 谢楠
- 课时:160h
- 价格 4580 元
特色双名师解密新课程高频考点,送国家电网教材讲义,助力一次通关
配套通关班送国网在线题库一套
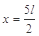 的直线,磁场方向垂直纸面向外.一质量为m、带电荷量为+q的粒子从y轴上P点以初速度v0垂直y轴射人匀强电场,在电场力作用下从x轴上Q点以与x轴正方向成450角进入匀强磁场.已知OQ=l,不计粒子重力.求:
的直线,磁场方向垂直纸面向外.一质量为m、带电荷量为+q的粒子从y轴上P点以初速度v0垂直y轴射人匀强电场,在电场力作用下从x轴上Q点以与x轴正方向成450角进入匀强磁场.已知OQ=l,不计粒子重力.求: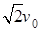 (2)
(2)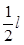 (3)
(3)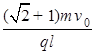
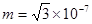 kg,电量q=-5×10-7 C。在该空间恰能做匀速直线运动。求:
kg,电量q=-5×10-7 C。在该空间恰能做匀速直线运动。求:
责编:郝悦浩
上一篇:物理:粒子在复合场中运动
下一篇:物理:电磁场的应用
| 课程专业名称 |
讲师 |
课时 |
查看课程 |
|---|
| 课程专业名称 |
讲师 |
课时 |
查看课程 |
|---|
点击加载更多评论>>